#Arquitectura
Este número no sólo ha sido encontrado de manera directa en teoría de proporciones… Uno de los modelos más conocidos da lugar a la conocida serie de Fibonacci.
Carlos Rosas Cancino / @CarlosRosas_C
carlos.rc@inperfecto.com.mx
El número áureo, tiene un significado importante en la naturaleza y derivado de ello ha permeado al diseño, como lo vamos a ver en el siguiente articulo que nos da muchos elementos para reconocer su importancia, disfrútenlo con nosotros.
EL NÚMERO ÁUREO: EN BÚSQUEDA DE LA PERFECCIÓN NATURAL
El número áureo, denotado también como, tiene un valor de (1 +√5) /2. Su nombre se ha propuesto en base a las iniciales de Pheidias, escultor griego, que supuestamente usó este número al construir el Partenón. Aunque no existe todavía un acuerdo sobre si ϕ aparece directamente dentro de las escalas fundamentales del Partenón, se sabe que aparece claramente en otras construcciones griegas (teatro Epidaurus, el teatro de Dionysus en Atenas.)

Algunas evidencias indican que los egipcios usaron esta proporción para sus construcciones, principalmente, en las pirámides, pero fue el matemático Euclides el que encontró una relación matemática fundamental para derivar su valor. En la proposición 30, de su libro 5, expone la construcción que representamos de la siguiente manera: Si denominamos como 1 a la longitud del segmento AB y como x al segmento AC, es fácil probar que la proporción entre el segmento largo, al segmento inmediatamente más corto, da lugar a la ecuación de segundo orden x2 – x + 1, que tiene como solución al número Φ.
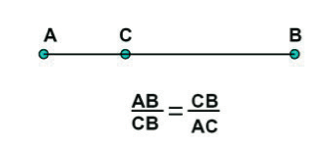
Esta proporción divide a un segmento en dos, uno más grande que el otro, dando lugar a un único valor. Esta relación se ha determinado en diferentes áreas de la ciencia como una manifestación esencial del balance y la proporción (especialmente en épocas antiguas y hasta el medioevo). Una de las obras de arte más admiradas por el mundo es la escultura El David, de Miguel Ángel, que se considera frecuentemente como una manifestación de la perfección. Esta obra maestra pone de manifiesto que muchas de las diferentes proporciones, dentro de lo que se consideró perfección en esa época, vienen dadas por Φ.
Este número no sólo ha sido encontrado de manera directa en teoría de proporciones, sino también en el ámbito de modelos de población. Uno de los modelos más conocidos da lugar a la conocida serie de Fibonacci, matemático italiano del siglo XII, que encontró una serie que reproducía naturalmente el valor de Φ. La serie se construye de la siguiente manera: “dados con los números 0 y 1, cada número de la serie es sencillamente la suma de sus dos inmediato predecesores, dando lugar a 0, 1, 1, 2, 3, 5, 8, 13, 21”, … Si tomamos la proporción entre dos números consecutivos de esta serie, en ella converge el númeroΦ.
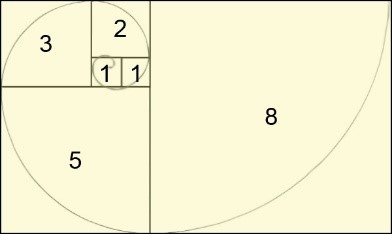
Aunque esta observación, sobre la serie de Fibonacci, es bastante interesante, es importante notar que también esta convergencia se da para cualquier serie que se construya como f(n + 1) = f(n) + f(n-1), lo que nos da a entender que el número está conectado a la forma en que las series se construyen y no a una construcción en particular.
La serie de Fibonacci es uno de los conjuntos de números que aparecen muy frecuentemente dentro de la naturaleza. Por ejemplo, el número de pétalos de muchísimas flores es un número de la serie. En crecimiento de plantas, el número de ramas que se van obteniendo a medida que el árbol crece es usualmente un número perteneciente a la serie 6 al cubo. Otro ejemplo típico es el cono de pino (o piña de pino). Un cono de pino se puede pensar como un conjunto de espirales que se van retorciendo hasta llegar a unirse en un punto que es el que se une al tallo. Hay ocho espirales en la dirección de las manecillas del reloj, mientras que hay 13 que se acercan más rápidamente a la punta en contra de las manecillas del reloj (situación muy similar se puede observar en una piña o en el girasol o en la coliflor).

La frecuencia con la que números pertenecientes a la serie de Fibonacci se manifiestan dentro de muchos objetos o situaciones en la naturaleza parecen indicar que hay algo intrínseco y óptimo que la naturaleza ha desarrollado ¿Por qué estos números se repiten en muchas plantas? ¿Por qué en la estructura de muchos moluscos o en la forma del ser humano? ¿Hay algo valioso en estas proporciones? Lo que sí es claro es que tiene muchas repercusiones en cómo la naturaleza se adapta a las condiciones del medio. De la misma manera que la serie de Fibonacci aparece en muchas realizaciones, también lo hace el número directamente. Este número se presenta muy frecuente en formas geométricas; por ejemplo, aparece como el valor de la diagonal de un pentágono regular de lado unidad, el rectángulo áureo (tome el rectángulo Φ con lados unidad y phi y trace internamente iterativamente rectángulos usando siempre el lado más corto del más reciente rectángulo trazado y defina los puntos de corte entre el anterior rectángulo y el nuevo. Esta construcción, debida al Físico Bernoulli da lugar a una espiral elíptica que también aparece en muchas formas de la naturaleza).
En el área de la anatomía, recientes estudios de un grupo ruso dirigidos por el Dr. Korotkov han demostrado que si se analizan las ondas del cerebro de pacientes con cierta manifestación de euforia, visualización muy activa o demasiado perceptivos, la proporción entre las ondas cerebrales esta dada por este número. Todos los eventos anteriormente descritos parecen indicar que la naturaleza ha desarrollado reglas que están enmarcadas dentro de la magia de las relaciones matemáticas, que la ayudan a optimizar sus esfuerzos y mejorar sus condiciones.
Vamos a enfocarnos más en la realizaciones de este número en el área de ciencia de materiales, que también manifiesta de manera unívoca, que las leyes de la física hacen uso del valor de , especialmente en cómo se maximiza o minimiza cierta propiedad, una estructura o una ley de comportamiento.
Dentro de la ciencia de materiales, centrémonos en la nanotecnología, área de creciente interés, tecnológico y científico, que pretende desarrollar dispositivos o estructuras a una escala nanométrica (un nanómetro es equivalente a 109 m que es un millón de veces más pequeño que un milímetro. Una manera sencilla de darse cuenta de estas dimensiones es pensar que esta escala se consigue logrando colocar 5 átomos de carbono en una línea).
Entre las muchas formas estructurales que se pueden obtener a esta escala, una de las que ha atraído enormemente la atención es la de los agregados metálicos. Los agregados, tal y como su nombre indica, son agrupaciones de átomos de unos pocos nanómetros de tamaño.
La parte más interesante es que estas estructuras poseen propiedades diferentes con respecto a sus contrapartes cristalinas (las propiedades electrónicas de agregados de oro son bastante diferentes de las del sistema cristalino, por ejemplo su color es diferente y depende del tamaño). Las formas estructurales que pueden adquirir son muy diversas, pero solo algunas predominan.
Sorprendentemente, éstas se pueden obtener como extensiones o realizaciones de los denominados sólidos platónicos. Éstos son básicamente poliedros regulares (un poliedro es un sólido con caras planas). La parte mas interesante es que estos poliedros se pueden relacionar al número Φ, que de nuevo, mágicamente, hace su aparición en las relaciones de estas formas geométricas.
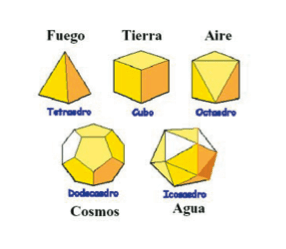
Por ejemplo, si se toman 3 rectángulos que siguen la relación del número áureo (la base es a la altura como el número de oro) y se intersectan a ángulos de noventa grados, obtenemos un objeto con 12 esquinas, si dibujamos en cada esquina un pentágono centrado en ellos, obtenemos un perfecto dodecaedro. Las doce esquinas también resultan ser las 12 esquinas en las que se unen los triángulos que forman el.
En el caso del poliedro de 120 lados, cada uno de los vértices se puede obtener como un múltiplo del número Dentro de este poliedro de 120 lados, se pueden circunscribir muchos otros, por lo que también pueden ser representados a partir del número. Esto explica en cierta manera que los sólidos platónicos contengan muchas de las estructuras que aparecen a escala nanoscópica y que el número contenga a todos los sólidos platónicos, dando una relación universal para entenderlos.
Una de las estructuras más famosas hoy en día, en el área de nanotecnología, es el fulereno de 60 átomos de Carbono (con un diámetro del orden de 7.5 x 10 -10 m), que se puede construir de manera muy sencilla: considere una pelota de fútbol que tiene un diámetro del orden de 22 cm, en cada vértice coloque un átomo de carbono y ahora escale esta forma a que tenga el diámetro del denominado fulereno.
Esta estructura también tiene una relación muy cercana al número Φ, ya que las coordenadas de cada una de las posiciones de los átomos se puede obtener como múltiplos del número Φ. Esta forma estructural de carbonos bastante estable tanto mecánicamente como electrónicamente. Es entonces de esperar que estructuras obtenidas bajo transformaciones en las que el número de oro aparece también se comporten de la misma manera.
Otro ejemplo en la física, donde estas relaciones aparecen de manera muy clara, es en las denominadas losetas de Penrose. El problema se propone de la siguiente manera: ¿Cómo podemos cubrir un espacio bidimensional usando sólo figuras geométricas de una cierta simetría? Hasta no hace muy poco se creía que solamente se podía hacer con formas de cierta simetría como se muestra en la figura 5. El caso de simetría cinco, es decir, con pentágonos. A primera vista uno decidiría que no se puede llenar un espacio bidimensional con esta forma. Recuerde que el número está asociado al pentágono en sí. Fue en los 70’s cuando el matemático Roger Penrose propuso una manera de poder hacerlo. Básicamente él encontró que la superficie se podía cubrir con formas geométricas basadas en el número que se conocen como losetas de Penrose.
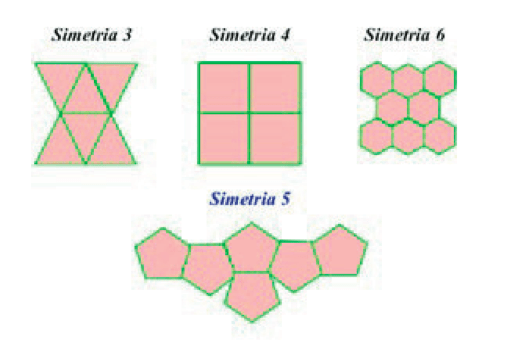
Una realización del recubrimiento espacial se muestra en la misma figura. Independientemente de cual de las losetas se use, al final se puede probar que para poder cubrir correctamente el espacio, la proporción de losetas de un tipo con respecto a otro converge de nuevo al número Φ. Aunque éste pareciera ser nada más una curiosidad matemática, resulta de gran actualidad en la ciencia de materiales, en los denominados cuasi-cristales, que son básicamente estructuras que no son completamente cristalinas y que presentan manifestaciones como las de sistemas desordenados (vidrios). Observados por primera vez en sistemas de aluminio-manganeso (Al6Mn), pero desde entonces han sido observados en muchos otros sistemas tales como: Nb- Fe, Al-Mg-Zn, Al-Ni-Co, V-Ni-Si, Cr-Ni, etc.

FUENTE
REVISTA DIGITAL UNIVERSITARIA
Volumen 6 Núm. 7
ISSN:1067-06079
http://www.revista.unam.mx/vol.6/num7/art68/int68.htmEL NÚMERO ÁUREO:
EN BÚSQUEDA DE LA PERFECCIÓN NATURAL
Aldo Humberto Romero
Castro Profesor Investigador Cinvestav-Queretaro. Qro, México. aromero@qro.cinvestav.mx