#Arquitectura
Los que poseen una mente dinamizada por los deleites de la literatura, forzosamente poseen en su corazón la imagen grabada de Ennio, como si fuera la de un dios, cincelada en la capilla de su corazón.
Carlos Rosas C / @CarlosRosas_C
carlos.rc@inperfecto.com.mx
El libro IX de los Diez Libros de Arquitectura es por demás interesante, el conocimiento y manejo de la astronomía parecería en este momento para el oficio de la arquitectura un instrumento en desuso, sin embargo a lo largo de esta obra podemos obtener muchas pruebas de lo contrario.
El movimiento de los astros representa no solo una maravilla en el imaginario colectivo, la utilidad que representa se podrá comprobar a lo largo de este libro, Vitruvio ha legado su conocimiento no solo para el deleite, sino para todo aquel que desee interesarse y voltear al cielo para conectar y materializar el conocimiento.
Nos acercamos al desenlace de una obra extraordinaria llena de conocimiento. Sigan con nosotros en el especial de arquitectura “En búsqueda de los maestros” sobre los Diez Libros de Arquitectura de Marco Vitruvio Polión.
LIBRO IX
INTRODUCCIÓN
Los antiguos griegos concedieron a los atletas más famosos, que habían alcanzado la victoria en los juegos Olímpicos, Píticos, Ístmicos y Nemeos, unos honores tan extraordinarios que no sólo recibían los aplausos del público en los escenarios cuando se levantaban con su palma y su corona, sino que, al volver victoriosos a sus propias ciudades, eran conducidos como triunfadores en una cuadriga hasta las calles de sus ciudades de origen y además estaban exentos de pagar ciertos impuestos durante toda su vida, como premio acordado por el Estado.

Al recapacitar ahora sobre estas costumbres, no deja de admirarme que no concedan honores similares, o aún mayores, a los escritores, que aportan innumerables beneficios a todos los pueblos y a lo largo de los tiempos. Ciertamente sería mucho mejor establecer esta costumbre, pues los atletas consiguen fortalecer simplemente sus músculos, mediante sus entrenamientos, pero los escritores no sólo perfeccionan su propia inteligencia sino también la de todos los hombres y con la información de sus libros fijan unas normas instructivas para alentar el talento y el ingenio de todos los hombres.

¿Qué utilidad ha proporcionado a la humanidad el hecho de que Milón de Crotona resultara invicto en todas sus competiciones?, ¿qué provecho han prestado otros muchos vencedores si no es el disfrutar de la fama entre sus conciudadanos mientras vivieron? Más las enseñanzas de Pitágoras, Demócrito, Platón, Aristóteles y de otros muchos pensadores, elaboradas día a día gracias a su incesante trabajo, han dado unos frutos nuevos y espléndidos tanto a sus propios conciudadanos como a todo el mundo. Quienes han degustado sobradamente sus abundantes enseñanzas desde su infancia, poseen una inmejorable sensibilidad intelectiva, establecen unas costumbres dignas y civilizadas en las ciudades, un cuerpo de derechos justos y unas leyes sin las que la ciudad no puede mantenerse a salvo.
Puesto que de la sabiduría de los escritores han emanado tan importantes beneficios para todos, tanto individual como colectivamente, en mi opinión deben concedérseles palmas y coronas y, además, se les debe tributar los honores del triunfo y juzgarlos dignos moradores de las mansiones de los dioses. Pasaré a exponer, a modo de ejemplo, algunas de sus ideas, simplemente de alguno de ellos, que han resultado prácticas y definitivas para la vida de los hombres; si se valoran en su justa medida, todo el mundo coincidirá en tributarles los honores que se merecen.

En primer lugar, comenzaré por una demostración de Platón, entre las muchas y muy útiles que él mismo explicó: si fuera necesario duplicar una superficie cuadrada, o bien un campo de lados iguales, como ello exigirla una cierta cantidad de números que las multiplicaciones aritméticas no nos posibilitarían hallarlos, encontramos la solución mediante una figura geométrica, delineada con toda exactitud. He aquí su demostración: un espacio cuadrangular cuyos lados midan diez pies, nos da una superficie de cien pies; si fuera preciso duplicarlos, es decir, hallar una superficie de doscientos pies a partir de un espacio de lados iguales, el problema sería descubrir la longitud de los lados de este cuadrado para obtener esos doscientos pies, que se corresponderían con el doble de la superficie propuesta. Imposible resolver este problema mediante la aritmética, pues si los lados tienen catorce pies de longitud, elevándolos al cuadrado nos dan ciento noventa y seis pies; si miden quince pies, nos dará doscientos veinticinco pies.
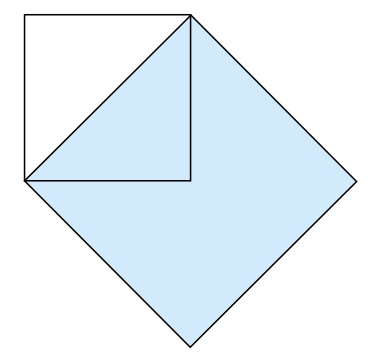
Por tanto, como por medio de la aritmética no se puede resolver, trácese una diagonal desde un ángulo hasta el otro sobre ese mismo cuadrado de diez pies de largo y de ancho, para que nos queden dos triángulos de la misma medida, esto es, que cada triángulo delimite una superficie de cincuenta pies; sobre la longitud de la diagonal describiremos un cuadrado de lados iguales; si en el cuadrado más pequeño han quedado delimitados dos triángulos de cincuenta pies, apoyándonos en la diagonal trazada nos quedarán en el cuadrado más grande cuatro triángulos de las mismas medidas, con el mismo número de pies. De esta manera demuestra Platón, mediante figuras geométricas, la duplicación de un cuadrado,
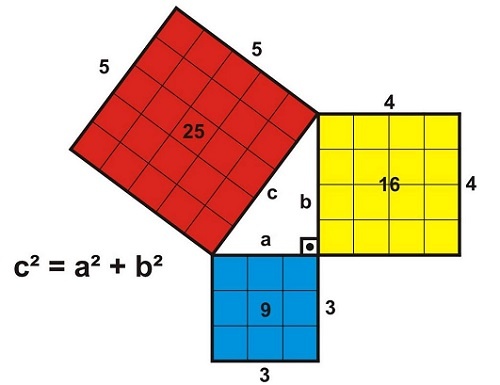
Pitágoras demostró el descubrimiento de la escuadra, sin necesidad de acudir a los artesanos. Los artesanos con serias dificultades logran fabricar una escuadra exacta echando muchas horas de trabajo y, sin embargo, sí se puede conseguir siguiendo el método y la normativa del mismo Pitágoras. Veamos el proceso: si se toman tres reglas, una de tres pies de longitud, otra de cuatro pies y la tercera de cinco pies y si las colocamos de manera que queden en contacto sus extremos, lograremos una figura triangular y formarán una escuadra perfecta.
Si se trazan unos cuadrados de lados iguales utilizando cada una de estas reglas, el cuadrado cuyos lados midan tres pies tendrá una superficie de nueve pies; si sus lados son de cuatro pies, su superficie medirá dieciséis pies, y si son de cinco pies, tendrá una superficie de veinticinco pies. El número total de pies, contenido en las superficies de los dos cuadrados de tres y cuatro pies de longitud, será el mismo que el número de pies que mida la superficie trazada midiendo cinco pies en cada lado.
Ante el hallazgo que acababa de descubrir, Pitágoras tuvo la convicción de haber sido inspirado por las mismas Musas y, lleno de agradecimiento -según dicen-, inmoló en su honor unas víctimas. Este hallazgo o descubrimiento resulta muy práctico en multitud de aspectos -en las medidas-, como es igualmente útil en la construcción de las escaleras de los edificios, ya que permite obtener una exacta proporción de los peldaños.
Si la altura del entramado o piso se divide en tres partes, desde lo alto de las vigas hasta el nivel del suelo, la pendiente del montante de la escalera deberá tener cinco de estas partes, para que posea la longitud exacta. Tomando la altura entre el techo y el nivel del suelo y de acuerdo con lo que midan las tres partes, desde la misma vertical retrotraeremos cuatro de estas partes y allí mismo colocaremos el pie inferior del montante de la escalera; de esta forma, nos quedará una justa proporción y los peldaños de la escalera estarán colocados adecuadamente.
Numerosos y admirables fueron los descubrimientos de Arquímedes, pero, de todos, el que muestra un ingenio más extraordinario es el que paso a exponer. Hierón fue elevado al poder real y había decidido colocar una corona de oro en un templo, como promesa a los dioses inmortales, por el éxito de sus victorias; mandó fabricarla, después de acordar el precio de su coste, y entregó al orfebre la cantidad de oro necesaria y exacta, pesándolo previamente. El orfebre presentó su trabajo terminado de manera primorosa ante el rey en el tiempo convenido y éste dio su aprobación; el rey ordenó que pesaran la corona y aparentemente se ajustaba al peso del oro entregado.
Poco después le informaron al rey, mediante una denuncia, que había sustituido cierta cantidad de oro por plata en la fabricación de la corona. Hierón se encolerizó al sentirse estafado, pero no encontraba la manera de descubrir el fraude, por lo que suplicó a Arquímedes que se responsabilizara de la investigación. Arquímedes se tomó con empeño este encargo; por pura casualidad, se dirigía al baño y cuando se introdujo dentro de la bañera observó que se derramaba fuera de la bañera una cantidad de agua proporcional al volumen de su cuerpo, que iba sumergiendo.
Esta puntual experiencia le hizo ver la solución del problema y, sin perder tiempo, lleno de alegría, saltó fuera de la bañera, desnudo se dirigió hacia su propia casa manifestando a todo el mundo que había encontrado lo que estaba buscando; corriendo gritaba una y otra vez «eureka», «eureka».

Entonces, siguiendo el curso de su descubrimiento, según dicen, se hizo con dos lingotes que tenían el mismo peso que la corona: uno de oro y otro de plata. Llenó de agua una gran vasija hasta los bordes e introdujo dentro el lingote de plata por lo que se desbordó fuera de la vasija una cantidad de agua igual al volumen del lingote que había introducido. Lo sacó de la vasija y la volvió a llenar hasta los bordes, como estaba en un principio, comprobando que la cantidad de agua derramada era un sextario. De esta manera descubrió que el peso de la plata se correspondía con una exacta cantidad de agua.
Después de esta experiencia, introdujo en la vasija llena de agua un lingote de oro; lo sacó posteriormente y volvió a llenarla hasta los bordes; observó que la cantidad de agua derramada era menor, concluyendo en qué exacta proporción el volumen del oro era menor que el de la plata, aunque pesaran lo mismo los dos lingotes. Finalmente, de nuevo llenó con agua la vasija, introdujo en su interior la corona y descubrió que se había desbordado más agua que al introducir el lingote de oro del mismo peso; partiendo de este hecho -se había derramado más agua al introducir la corona que el lingote- y haciendo cálculos, descubrió que la corona contenía una aleación de plata y de oro; así puso en evidencia el fraude cometido con el orfebre.

Vamos a poner ahora nuestra atención en los hallazgos de Architas de Tarento y de Eratóstenes de Cirene; los descubrimientos de estos pensadores fueron muy numerosos y muy útiles para la humanidad, precisamente por la aplicación de las matemáticas. Merecen nuestro más sincero agradecimiento por sus trabajos de investigación, pero sobre todo admiramos sus controversias en la resolución de un problema muy concreto: cada uno ofreció una explicación y un método diferentes a la orden que había mandado Apolo por medio de sus oráculos en Delfos; he aquí su orden: «los habitantes de la isla quedarían libres de la reprobación divina si duplicaban el número de pies cúbicos que tenía su propio altar».
Arquitas, mediante unos gráficos de semicilindros, y Eratóstenes, mediante un instrumento muy simple -el mesolabio-, resolvieron el mismo problema. Como tales teorías han sido resueltas con el profundo placer que nos brindan las ciencias, no nos queda más alternativa que confesar nuestra emoción ante estos hallazgos, al considerar las consecuencias y los efectos de cada una de estas soluciones tan inventivas.

Examinando otros muchos escritos, me causa una especial admiración Demócrito, con sus libros sobre la naturaleza de las cosas, y en concreto su comentario titulado «Cosas y trucos hechos a mano»; lo que él había experimentado personalmente lo marcaba con su anillo haciendo una señal sobre la cera blanda.
Por todo ello, las sugerencias de hombres tan notables no sólo son perfectamente eficaces para mejorar las costumbres, sino que además prestan un gran servicio a todos los hombres, cuando el prestigio que consiguen los atletas se desvanece en breves años, al compás del declive de sus facultades físicas; ni en los momentos de mayor éxito, ni en los años posteriores brindan un servicio a la humanidad comparable a las ideas y a la imaginación de los sabios.
Aunque no se tributan honores ni a las costumbres ni a los principios inmejorables de tales escritores, sus propias mentes les proyectan a contemplar el más alto cielo, elevándolos gradualmente hasta la cúspide celeste, para memorial de todos. Los hombres, sus ideas y su figura, inevitablemente son conocidos y familiares a la posteridad. Los que poseen una mente dinamizada por los deleites de la literatura, forzosamente poseen en su corazón la imagen grabada de Ennio, como si fuera la de un dios, cincelada en la capilla de su corazón. Quienes saborean con dulzura y atención los poemas de Accio, creen mantener muy presente la fuerza de sus palabras, su propia imagen y su propio retrato.
Igualmente, otras muchas generaciones que nos sucederán tendrán también la impresión de que están discutiendo con Lucrecio sobre el tema de la naturaleza de las cosas; sobre el arte de la oratoria con Cicerón, y con Varrón conversarán sobre la lengua latina muchas generaciones futuras; habrá muchos filólogos y eruditos que, deliberando en profundidad sobre temas diversos con filósofos griegos, tendrán la impresión de mantener conversaciones personales con ellos; en fin, las ideas y los pensamientos de estos sabios escritores que, aunque físicamente no están presentes, sin embargo se hacen presentes de modo brillante cuando son citados en las discusiones y en las investigaciones, poseen más entidad y eficacia que las opiniones de los que están presentes.

Así, César, con el apoyo de tales autores y sirviéndome de su inteligencia y de sus consejos, he redactado estos volúmenes: en los siete primeros libros he tratado el tema de la construcción de los edificios; en el octavo, expuse el tema del agua, y en este noveno libro trataré sobre la gnomónica y su descubrimiento a partir de los rayos del sol en el mundo y a partir de las sombras que proyecta el gnomon; explicaré también la proporción en la que las sombras se prolongan o disminuyen.




