#Arquitectura
Se le ha llamado de varias maneras, sin embargo su presencia en la naturaleza, las matemáticas, y el arte la convierten en protagonista de este mundo.
Carlos Rosas C / @CarlosRosas_C
carlos.rc@inperfecto.com.mx
Una de las herramientas en las que el arquitecto se apoya es la proporción. Dicha herramienta no se encuentra directamente relacionada con el funcionamiento de los espacios, sin embargo, forma parte de la percepción con la que los espacios se componen entre si para darle el valor agregado de la belleza.
La escala de un acceso, de una plaza, de una sala de estar, de una fuente etc. preferentemente deberían encontrarse en relación unas con otras ya que siendo concebidos para servir al hombre tambien deben estar en función a el.
De manera figurada los espacios arquitectónicos tambien respiran, expresan, y manifiestan ambientes particulares que cada usuario les asigna, algunos muy simplistas y otros hasta poéticos, para ello también entran en escena la luz, el color, las texturas etc.
La Sección Áurea juega un papel muy importante en la composición arquitectónica, y aunque dentro de la práctica del día a día ha llegado a caer en desuso, el carácter de la proporción áurea no es limitativo al campo de la arquitectura ya que dentro del infinito campo de las artes se encuentra presente, empezando porque dentro de los patrones que la naturaleza ocupa para logar una eficiencia magnífica de la cual mediante la observación y análisis muchos personajes destacados lograron trasladarla para crear piezas magníficas. Demos paso a la Sección Áurea para ver que tan presente se encuentra en nuestra vida diaria.
ORÍGENES Y REFERENCIAS
El origen exacto del término Sección Áurea es bastante incierto. Generalmente se sitúa en Alemania, en la primera mitad del siglo XIX. Muchos han sido los artistas, humanistas y matemáticos que lo han tratado, aunque bajo distinto sobrenombre y con distinta disposición. Otros nombres que recibe son Sección Divina, Sección de Oro, Proporción Divina, Proporción Dorada, Canon Áureo, Regla de Oro o Número de Oro.
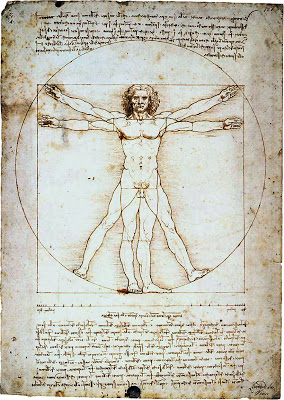
Sección Áurea es simplemente una proporción concreta. Esta proporción ha desempeñado un importante papel en los intentos de encontrar una explicación matemática a la belleza, de reducir ésta a un número, de encontrar “ la cifra ideal “.

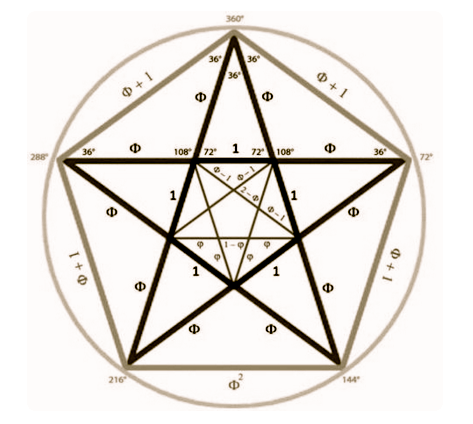
De esta proporción hablaban ya desde mucho tiempo atrás, los egipcios, la descubrieron buscando medidas que les permitieran dividir la tierra de forma exacta. De Egipto pasó a Grecia y de allí a Roma. Pitágoras (569 a.C.) escogió como símbolo para su Escuela la estrella pentagonal, figura geométrica que muestra en todas sus relaciones la sección áurea y se cree que a partir de esta figura llegaron a la noción de inconmensurabilidad y al conocimiento de los números inconmensurables, tales como el que ahora nos ocupa.
Platón (428-347 a.C.) hace referencia a ella en el Timeo y dice “es imposible combinar bien dos cosas sin una tercera, hace falta una ligazón entre ellas que las ensamble, la mejor ligazón para esta relación es el todo…”. Euclides (450-380 a. C.), matemático griego, en su obra principal Elementos, extenso tratado de matemáticas sobre geometría plana, proporciones, propiedades de los números, magnitudes inconmensurables y geometría del espacio, nos revela la primera fuente documental importante sobre esta sección, su cálculo y trazado geométrico. Más tarde, Vitruvio, arquitecto romano, vuelve a tratarla en sus Diez libros de arquitectura.

En el periodo renacentista existen numerosos autores que retoman este canon. El monje Franciscano Luca Pacioli (1445-1514) la denominaba “Divina Proporción” y escribe todo un tratado (De Divina Proportione), sobre sus propiedades y proporciones. Este tratado se apoyaba en las ideas de Piero della Francesca (1420-1492), quien había expuesto en De Abaco, manual de matemáticas para comerciantes, el cálculo de proporciones. Otros artistas como Leonardo da Vinci (1452-1519) o Alberto Durero (1417-1528) hicieron especial hincapié en la relación del número áureo y las proporciones humanas y elogiaron la apariencia de armonía y equilibrio que presentan las obras creadas a partir e dicha proporción. Andrea Palladio (1508-1580), arquitecto italiano, estaba convencido de que las escalas musicales -relacionadas con la sección áurea- han de usarse como cánones de diseño arquitectónico. Uno de los últimos renacentistas que celebraron sus virtudes fue Kepler (1517-1630), quien afirmaba: “hay dos tesoros en la geometría… uno el teorema de Pitágoras y otro la división proporcional… una joya”.

Después esta regla divina cayó en el olvido hasta el siglo XIX. En este periodo vuelve a ser puesta de relieve como principio morfológico por el alemán Adolf Zeysing, quien en 1855 afirma en su Aestetische Forschungen: “Para que un todo, dividido en partes desiguales, parezca hermoso, desde el punto de vista de la forma, debe haber entre la parte menor y la mayor, la misma razón que entre la mayor y el todo”. En este mismo siglo, pintores como Seurat (1859- 1891) o Cézanne (1839-1906) volvieron a buscar la armonía y la belleza en el arte por medio de estrictas reglas geométricas, entre ellas, la regla áurea. En la arquitectura, destacamos sin duda a Le Corbusier (1887-1965) que en su empeño de considerar a la naturaleza como encarnación de todo lo verdadero, quiere traducir las leyes que la rigen en proporciones geométricas simples y tomarlas como cánones de diseño universal, haciendo así que toda obra creada por el hombre, refleje la naturaleza misma de éste.
Hoy en día son muchos los artistas que usa esta proporción para estructurar sus obras, ya sea de forma consciente e inconscientemente, debido al bagaje cultural de siglos.
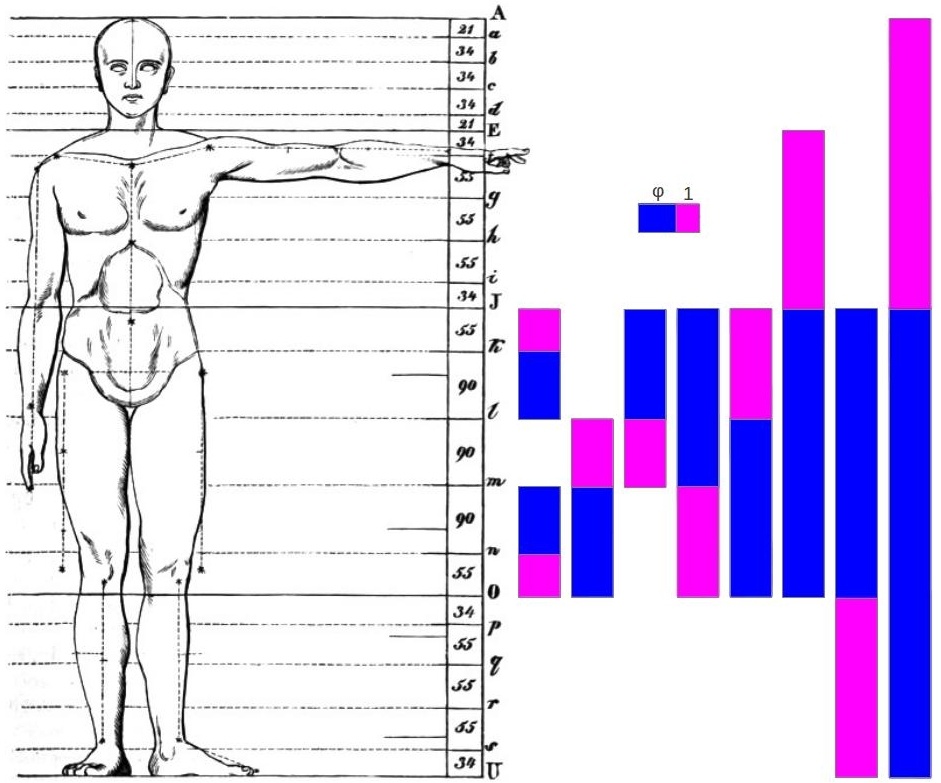
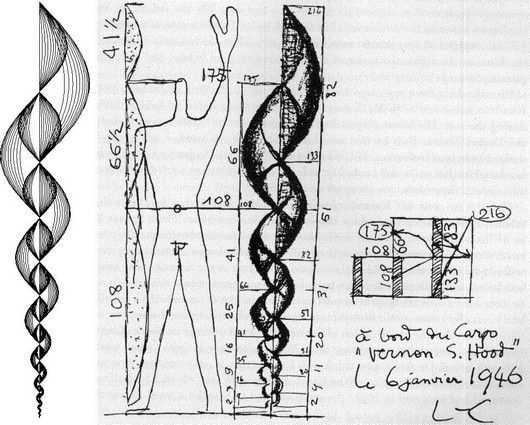
DEFINICIÓN MATEMÁTICA
La sección áurea del latín sectio aurea es una proporción que aparece entre los segmentos de una recta al dividir ésta en media y extrema razón. Una recta AB queda dividida por un punto F en otros dos segmentos (AF y FB) de tal forma que el segmento mayor es al menor, como el todo es al mayor.
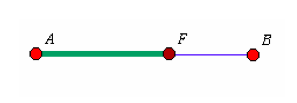
Tan solo existe un punto F que haga posible esta relación entre los segmentos y verifique la proporción AF /FB = AB /AF, que también podemos escribir como AF /FB = (AF+FB) /AF.
Si hacemos AF = x y FB =1, tenemos:
x2 x1
x2 −x−10
x15 2
Eligiendo la solución positiva tenemos:
x ( 5 1)/2 1,6180339885 …
Éste es El Número de Oro, que normalmente designamos con la letra griega ϕ Su característica principal es la inconmensurabilidad, es decir, no se puede expresar como proporción de dos enteros, es irracional. El periodo de este numero es infinito y sus cifras decimales no se repiten periódicamente. Este número tiene propiedades únicas, algunas de ellas las veremos a continuación.
De las expresiones anteriores tenemos:

Podemos también obtener otra expresión del número de oro, dividiendo por √ los dos miembros de la igualdad:
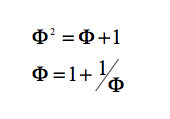
sustituyendo de forma reiterada ϕ por su valor, tenemos:
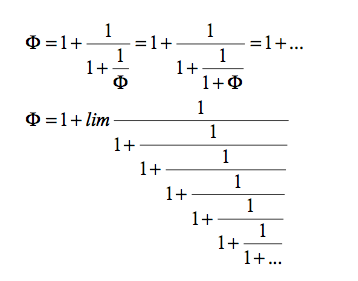
por lo que:
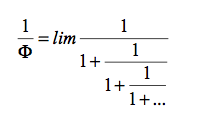
Estos desarrollos del número Φ en fracción continua se conocen desde la antigüedad, pero la expresión del límite de la raíz cuadrada resulta de un teorema publicado en 1917 en la Universidad de Oklahoma por Nathan Altshiller-Court, como indica Matila en su libro Estética de las proporciones en la naturaleza y en las artes.
Estimado lector…
En la siguiente entrega vamos a continuar con éste tema que nos irá dando a conocer los secretos que guarda la Proporción Divina, no se lo pierdan.
#InPerfecto
FUENTE
SECCIÓN ÁUREA EN ARTE, ARQUITECTURA Y MÚSICA
YOLANDA TOLEDO AGÜERO
http://matematicas.uclm.es/ita-cr/web_matematicas/trabajos/240/La_seccion_aurea_en%20arte.pdf




